「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
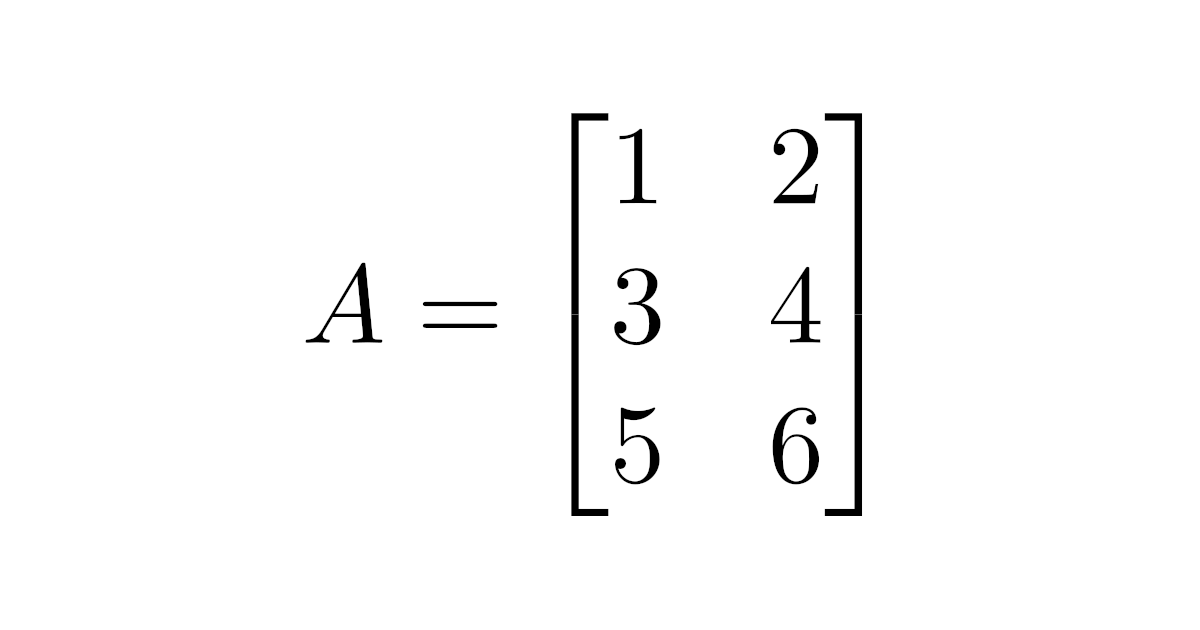 線形代数学の基本
線形代数学の基本 「線形代数学の基本」の一連の記事
 線形代数学の基本
線形代数学の基本 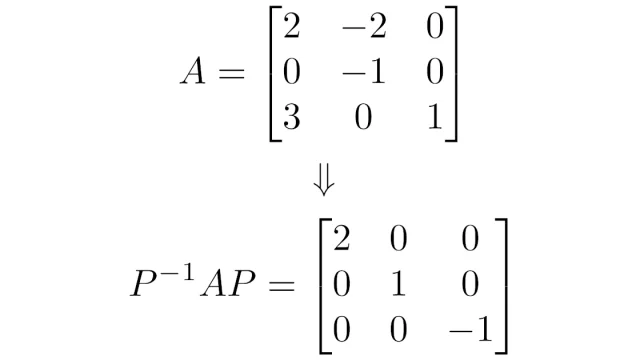 線形代数学の基本
線形代数学の基本 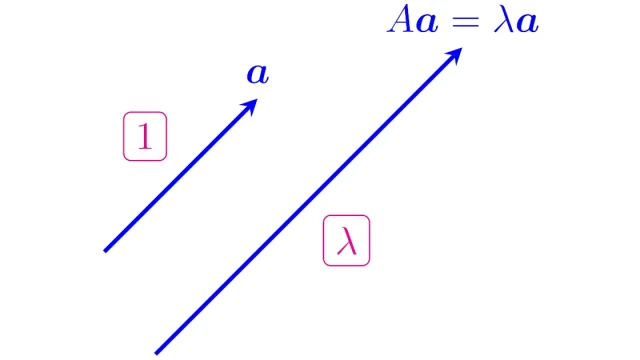 線形代数学の基本
線形代数学の基本 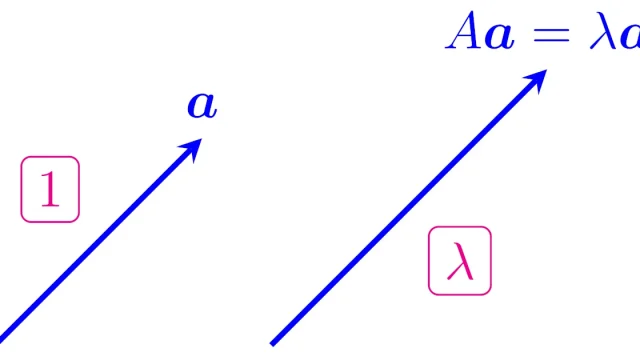 線形代数学の基本
線形代数学の基本 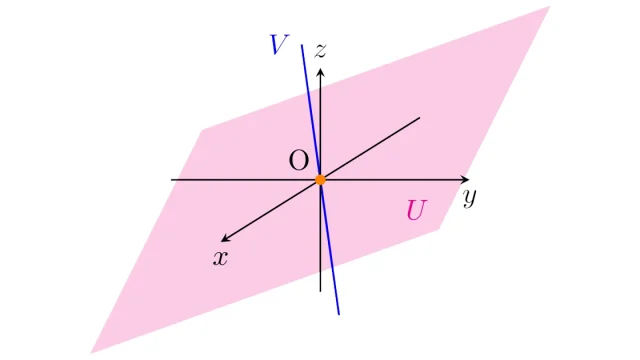 線形代数学の基本
線形代数学の基本 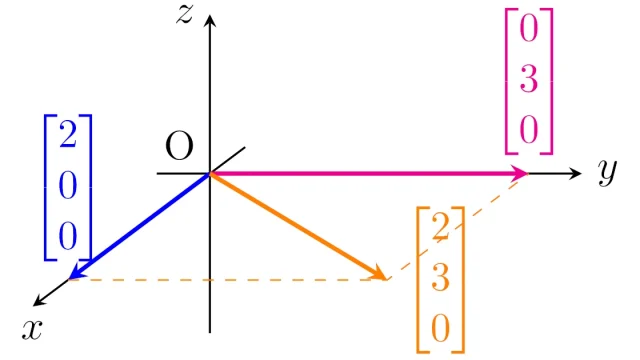 線形代数学の基本
線形代数学の基本 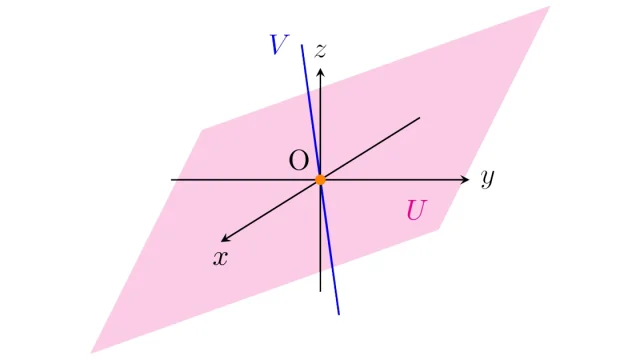 線形代数学の基本
線形代数学の基本 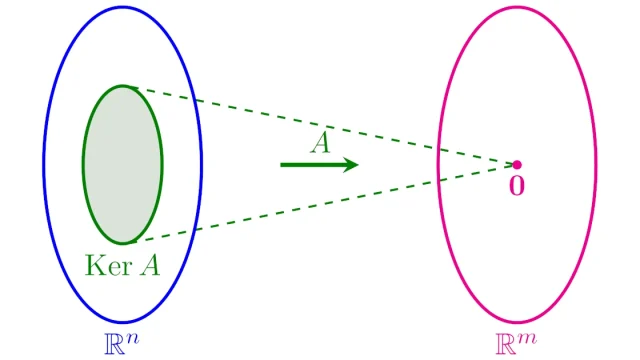 線形代数学の基本
線形代数学の基本 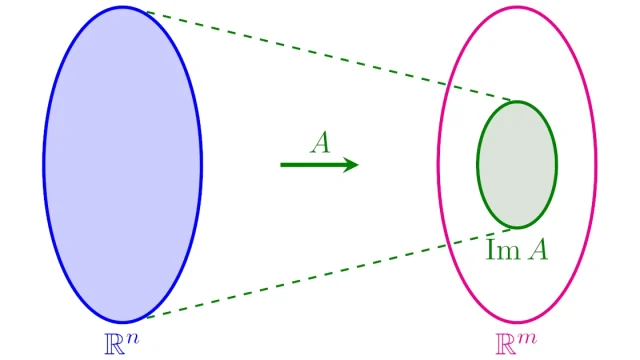 線形代数学の基本
線形代数学の基本 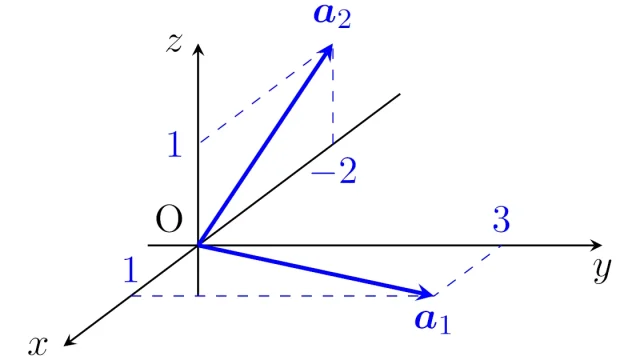 線形代数学の基本
線形代数学の基本