正方行列$A$に対して,$AB=BA=I$となる正方行列$B$が存在するとき,$A$を正則行列といい,$B$を$A$の逆行列といって$A^{-1}$と表すのでした.
正方行列の正則性の判定法は様々ありますが,それらのひとつに行列式を用いた判定法があり,
- $A$が正則行列であること
- 行列式$|A|$が0でないこと
が同値となります(証明は次の記事).そのため,行列式を計算できることは大切です.
この記事では
- 準備(置換の集合$S_n$の性質)
- 行列式の基本性質
- 行列式を具体例に計算する方法
を順に解説します.
なお,この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが,複素行列など一般の体を成分とする行列・ベクトルに対しても同様です.
この記事では$n$を2以上の整数とし,$\{1,\dots,n\}$の置換全部の集合を$S_n$と表します.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
準備(置換の集合$S_n$の性質)
まずは行列式の性質を示す際に必要となるいくつかの補題を用意しておきます.
補題1(逆置換の集合)
置換$\sigma$を$S_n$全体で漏れなく重複なく動かすとき,逆置換$\sigma^{-1}$も$S_n$全体を漏れなく重複なく動きます.
[補題1]$S_n=\set{\sigma^{-1}}{\sigma\in S_n}$が成り立つ.
任意の$\sigma\in S_n$に対して,$\sigma$は全単射だから$\sigma^{-1}\in S_n$である.$S_n$は有限集合なので,
\begin{align*}S_n\to S_n;\sigma\longmapsto\sigma^{-1}\end{align*}
が単射であることを示せばよい.$\sigma,\tau\in S_n$が$\sigma^{-1}=\tau^{-1}$を満たせば,
\begin{align*}\sigma=(\sigma^{-1})^{-1}=(\tau^{-1})^{-1}=\tau\end{align*}
が成り立つ.よって,単射なので$S_n=\set{\sigma^{-1}}{\sigma\in S_n}$が従う.
補題2(置換の積の集合)
置換$\sigma\in S_n$を固定し,置換$\tau$を$S_n$全体で漏れなく重複なく動かすとき,置換の積$\sigma\tau$, $\tau\sigma$も$S_n$全体を漏れなく重複なく動きます.
[補題2]任意の$\sigma\in S_n$に対して,$S_n=\set{\sigma\tau}{\tau\in S_n}=\set{\tau\sigma}{\tau\in S_n}$が成り立つ.
任意の$\tau\in S_n$に対して,$\tau$は全単射だから$\sigma\tau$も全単射なので,$\sigma\tau\in S_n$である.$S_n$は有限集合なので,
\begin{align*}S_n\to S_n;\tau\longmapsto\sigma\tau\end{align*}
が単射であることを示せばよい.$\tau,\iota\in S_n$が$\sigma\tau=\sigma\iota$を満たせば,
\begin{align*}\tau=(\sigma^{-1}\sigma)\tau=\sigma^{-1}(\sigma\tau)=\sigma^{-1}(\sigma\iota)=(\sigma^{-1}\sigma)\iota=\iota\end{align*}
が成り立つ.よって,単射なので$S_n=\set{\sigma\tau}{\tau\in S_n}$が従う.同様に$S_n=\set{\tau\sigma}{\tau\in S_n}$も従う.
置換の符号の性質
任意の$\sigma,\tau\in S_n$に対して,以下が成り立つ.
\begin{align*}&\sgn{(\sigma)}\sgn{(\tau)}=\sgn{(\sigma\tau)}=\sgn{(\tau\sigma)},
\\&\sgn(\sigma)=\sgn(\sigma^{-1})\end{align*}
が成り立つ.
$\sigma$, $\tau$がそれぞれ$k$個の互換の積,$\ell$個の互換の積で表されるとすると,$\sigma\tau$, $\tau\sigma$はいずれも$k+\ell$個の互換の積で表せるから,
\begin{align*}&\sgn{(\sigma)}=(-1)^k,\quad
\sgn{(\tau)}=(-1)^\ell,
\\&\sgn{(\sigma\tau)}=\sgn{(\tau\sigma)}=(-1)^{k+\ell}\end{align*}
が成り立つ.よって,
\begin{align*}\sgn{(\sigma)}\sgn{(\tau)}=\sgn{(\sigma\tau)}=\sgn{(\tau\sigma)}\end{align*}
が成り立つ.
また,$\tau=\sigma^{-1}$とすると$\sigma\tau$は単位置換なので$\sgn{\sigma}\sgn{\sigma^{-1}}=1$となるから,$(\sgn{\sigma},\sgn{\sigma^{-1}})=(\pm1,\pm1)$(複号同順)である.
よって,$\sgn{\sigma}=\sgn{\sigma^{-1}}$が従う.
行列式の基本性質
行列式の基本性質として,転置行列の行列式・行列式の交代性・行列式の線形性・積の行列式を説明します.
行列を転置しても行列式は変わらない
行列式は転置行列にしても変わりません.
正方行列$A$に対して,$|A|=|A^T|$が成り立つ.
$A=(a_{ij})$を$n$次正方行列とする.任意の$\sigma\in S_n$に対して$\{1,\dots,n\}=\{\sigma(1),\dots,\sigma(n)\}$だから
\begin{align*}a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}=a_{\sigma^{-1}(1)1}a_{\sigma^{-1}(2)2}\dots a_{\sigma^{-1}(n)n}\end{align*}
なので
\begin{align*}|A|&=\sum_{\sigma\in S_n}\sgn{(\sigma)}a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}
\\&=\sum_{\sigma\in S_n}\sgn{(\sigma)}a_{\sigma^{-1}(1)1}a_{\sigma^{-1}(2)2}\dots a_{\sigma^{-1}(n)n}
\\&=\sum_{\sigma\in S_n}\sgn{(\sigma)}a_{\sigma(1)1}a_{\sigma(2)2}\dots a_{\sigma(n)n}=|A^{T}|\end{align*}
が従う.なお,3行目最初の等号については,上の置換の[補題1]より$S_n=\set{\sigma^{-1}}{\sigma\in S_n}$だから和として等しい.
この命題から行列式について行で成り立つ性質は列でも成り立ち,逆に行列式について列で成り立つ性質は行でも成り立つことになりますね.
行列式の交代性(行または列を入れ替えたときの変化)
次の命題の性質を行列式の交代性(反対称性, antisymmetry)といいます.
$n$次正方行列$A=[\m{a}_1,\dots,\m{a}_n]$と$\sigma\in S_n$に対して,以下が成り立つ.
\begin{align*}|A|=\sgn{(\sigma)}|\m{a}_{\sigma(1)},\dots,\m{a}_{\sigma(n)}|\end{align*}
$A=(a_{ij})$とする.置換の性質より
\begin{align*}&\sgn{(\sigma)}|\m{a}_{\sigma(1)},\dots,\m{a}_{\sigma(n)}|
\\&=\sgn{(\sigma)}\sum_{\tau\in S_n}\sgn(\tau)a_{1\tau\sigma(1)}\dots a_{n\tau\sigma(n)}
\\&=\sum_{\tau\sigma\in S_n}\sgn{(\tau\sigma)}a_{1\tau\sigma(1)}\dots a_{n\tau\sigma(n)}=|A|\end{align*}
が従う.なお,3行目最初の等号については,上の置換の[補題2]より$S_n=\set{\tau\sigma}{\tau\in S_n}$だから和として等しい.
この命題から,次の系が容易に得られます.
等しい2つの列をもつ正方行列の行列式は0である.
$n$次正方行列$A=[\m{a}_1,\dots,\m{a}_n]$について,$i,j\in\{1,\dots,n\}$($i<j$)が$\m{a}_i=\m{a}_j$を満たすとする.互換$\sigma:=(i,j)\in S_n$について,行列式の交代性から
\begin{align*}|A|&=\sgn(\sigma)|\m{a}_{\sigma(1)},\dots,\m{a}_{\sigma(i)},\dots,\m{a}_{\sigma(j)},\dots,\m{a}_{\sigma(n)}|
\\&=-|\m{a}_1,\dots,\m{a}_j,\dots,\m{a}_i,\dots,\m{a}_n|
\\&=-|\m{a}_1,\dots,\m{a}_i,\dots,\m{a}_j,\dots,\m{a}_n|=-|A|\end{align*}
だから,$|A|=0$が従う.
行列式の線形性(行または列とスカラー倍をバラせる)
次の命題の性質を行列式の(多重)線形性(linearity)といいます.
$p,q\in\R$, $i\in\{1,\dots,n\}$とする.$n$次正方行列の行列式について,以下が成り立つ.
\begin{align*}&|\m{a}_1,\dots,\m{a}_{i-1},p\m{b}_i+q\m{c}_i,\m{a}_{i+1},\dots,\m{a}_n|
\\&=p|\m{a}_1,\dots,\m{a}_{i-1},\m{b}_i,\m{a}_{i+1},\dots,\m{a}_n|
\\&\quad+q|\m{a}_1,\dots,\m{a}_{i-1},\m{c}_i,\m{a}_{i+1},\dots,\m{a}_n|\end{align*}
任意の$k=1,\dots,i-1,i+1,\dots,n$に対して$\m{a}_k=\bmat{a_{1k}\\\vdots\\a_{nk}}$とし,$\m{b}_i=\bmat{b_{1i}\\\vdots\\b_{ni}}$, $\m{c}_i=\bmat{c_{1i}\\\vdots\\c_{ni}}$とすると,行列式の定義より
\begin{align*}&|\m{a}_1,\dots,p\m{b}_i+q\m{c}_i,\dots,\m{a}_n|
\\&=\sum_{\sigma\in S_n}\sgn(\sigma)a_{1\sigma(1)}\dots(pb_{i\sigma(i)}+qc_{i\sigma(i)})\dots a_{n\sigma(n)}
\\&=p\sum_{\sigma\in S_n}\sgn(\sigma)a_{1\sigma(1)}\dots b_{i\sigma(i)}\dots a_{n\sigma(n)}
\\&\quad+q\sum_{\sigma\in S_n}\sgn(\sigma)a_{1\sigma(1)}\dots c_{i\sigma(i)}\dots a_{n\sigma(n)}
\\&=p|\m{a}_1,\dots,\m{b}_i,\dots,\m{a}_n|+q|\m{a}_1,\dots,\m{c}_i,\dots,\m{a}_n|\end{align*}
が従う.
積の行列式は行列式の積に等しい
任意の$n$次正方行列$A,B$に対し,$|AB|=|A||B|$が成り立つ.
$A=(a_{ij})=[\m{a}_1,\dots,\m{a}_n]$, $B=(b_{ij})=[\m{b}_{1},\dots,\m{b}_{n}]$とすると,行列式の線形性より
\begin{align*}|AB|&=\abs{[\m{a}_1,\dots,\m{a}_n]\bmat{b_{11}&\dots&b_{1n}\\\vdots&\ddots&\vdots\\b_{n1}&\dots&b_{nn}}}
\\&=\abs{\sum_{k_{1}=1}^{n}b_{k_{1}1}\m{a}_{k_{1}},\dots,\sum_{k_{n}=1}^{n}b_{k_{n}n}\m{a}_{k_{n}}}
\\&=\sum_{k_{1}=1}^{n}\dots\sum_{k_{n}=1}^{n}b_{k_{1}1}\dots b_{k_{n}n}|\m{a}_{k_{1}},\dots,\m{a}_{k_{n}}|\end{align*}
である.もし$k_{1},\dots,k_{n}$の中に同じものがあれば,交代性の系から$|\m{a}_{k_{1}},\dots,\m{a}_{k_{n}}|=0$だから
\begin{align*}|AB|&=\sum_{\substack{\{k_{1},\dots,k_n\}\\=\{1,\dots,n\}}}b_{k_{1}1}\dots b_{k_{n}n}|\m{a}_{k_{1}},\dots,\m{a}_{k_{n}}|
\\&=\sum_{\sigma\in S_{n}}b_{\sigma(1)1}\dots b_{\sigma(n)n}|\m{a}_{\sigma(1)},\dots,\m{a}_{\sigma(n)}|
\\&=\sum_{\sigma\in S_{n}}\sgn{(\sigma)}b_{\sigma(1)1}\dots b_{\sigma(n)n}\cdot\sgn{(\sigma)}|\m{a}_{\sigma(1)},\dots,\m{a}_{\sigma(n)}|
\\&=|A|\sum_{\sigma\in S_{n}}\sgn{(\sigma)}b_{\sigma(1)1}\dots b_{\sigma(n)n}=|A||B^{T}|=|A||B|\end{align*}
となる.
$n$次正則行列$A$に対して,$|A^{-1}|=|A|^{-1}$が成り立つ.
$AA^{-1}=I$だから$|A||A^{-1}|=|AA^{-1}|=|I|=1$となって,$|A^{-1}|=|A|^{-1}$が成り立つ.
行列式を具体例に計算する方法
最後に,具体的に成分で与えられた行列式を具体的に計算する実用的な方法を紹介します.
簡単に次数を下げられる形の行列式
以下の命題は行列式の定義を適用すればすぐに得られるものですが,行列式を具体的に求める際に非常に有用な性質です.
$a_{1j}=0$($j=2,\dots,n$)を満たす$n$次正方行列$A=(a_{ij})$について,以下が成り立つ.
\begin{align*}|A|=\vmat{a_{11}&0&\dots&0\\a_{21}&a_{22}&\dots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\dots&a_{nn}}
=a_{11}\vmat{a_{22}&\dots&a_{2n}\\\vdots&\ddots&\vdots\\a_{n2}&\dots&a_{nn}}\end{align*}
仮定より$\sigma(1)\neq1$なら$a_{1\sigma(1)}=0$だから$a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}=0$なので
\begin{align*}|A|&=\sum_{\sigma\in S_n}\sgn(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}
\\&=a_{11}\sum_{\substack{\sigma\in S_n\\\sigma(1)=1}} \sgn(\sigma)a_{2\sigma(2)}\dots a_{n\sigma(n)}\end{align*}
である.$\set{\sigma\in S_n}{\sigma(1)=1}$は$\{2,\dots,n\}$の置換全体の集合なので,$S_{n-1}$と同一視できるから
\begin{align*}a_{11}\sum_{\substack{\sigma\in S_n\\\sigma(1)=1}}\sgn(\sigma)a_{2\sigma(2)}\dots a_{n\sigma(n)}
=a_{11}\vmat{a_{22}&\dots&a_{2n}\\\vdots&\ddots&\vdots\\a_{n2}&\dots&a_{nn}}\end{align*}
となる.
この命題を用いるには$a_{1j}=0$($j=2,\dots,n$)になっていることが必要なので,行列式をこの形に変形する必要がありますね.
基本変形による行列の変化
そこで行列の基本変形に関する次の命題が非常に便利です.証明はこれまでに示した性質からできます.
行列式について,次が成り立つ.
- 2つの列を入れ替えると,行列式の値は$-1$倍になる.
- 任意の列を$c$倍すると,行列式の値は$c$倍になる.
- 任意の列に他の列の何倍かを加えても行列式の値は変わらない.
(1)は行列式の交代性より成り立ち,(2)は行列式の線形性より成り立つ.以下,(3)を示す.
$c\in\R$, $k,\ell\in\{1,2,\dots,n\}$($k\neq\ell$)に対して,$A=[\m{a}_1,\dots,\m{a}_n]$の第$k$列の$c$倍を第$\ell$列に加えた行列の行列式は,行列式の線形性と交代性の系より
\begin{align*}&|\m{a}_1,\dots,\m{a}_{\ell}+c\m{a}_k,\dots,\m{a}_n|
\\&=|\m{a}_1,\dots,\m{a}_{\ell},\dots,\m{a}_n|+c|\m{a}_1,\dots,\m{a}_k,\dots,\m{a}_k,\dots,\m{a}_n|
\\&=|\m{a}_1,\dots,\m{a}_n|+c\cdot 0=|A|\end{align*}
となる.
行列を転置しても行列式は変わらないのでしたから,この命題の「列」を全て「行」に読み替えても成り立ちます.
行列式の具体的な計算例
行列式$\vmat{-22&-5&-7\\-11&-1&-3\\22&9&17}$を計算せよ.
基本変形と行列式の関係より
\begin{align*}\vmat{-22&-5&-7\\-11&-1&-3\\22&9&17}&=11\vmat{-2&-5&-7\\-1&-1&-3\\2&9&17}
\\&=11\vmat{2&5&7\\1&1&3\\2&9&17}=11\vmat{0&3&1\\1&1&3\\0&7&11}
\\&=-11\vmat{1&1&3\\0&3&1\\0&7&11}=-11\cdot1\vmat{3&1\\7&11}
\\&=-11\cdot(3\cdot11-1\cdot7)=-286\end{align*}
と計算できますね.

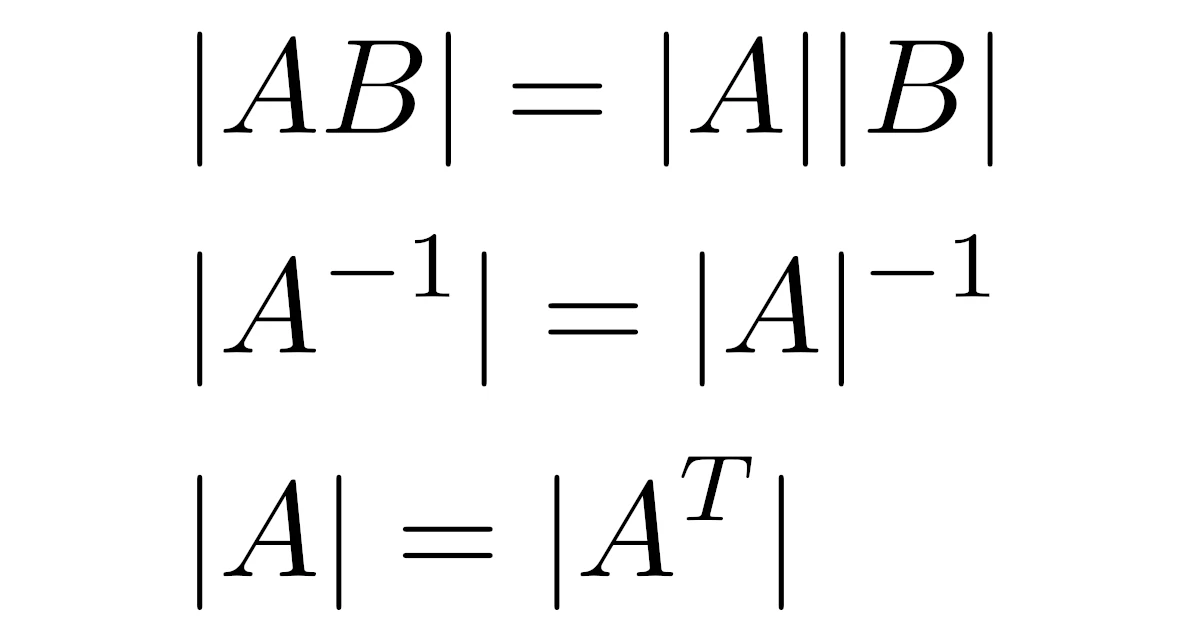


コメント