前々回の記事で行列式を定義し,前回の記事で基本的な行列式の性質を説明しました.
行列式を用いることで正方行列が正則であるかどうかの判定ができ,行列式は線形代数では非常に重要な道具となっています.
結論から言えば
- $|A|\neq0$
- $A$が正則であること
が同値となります.
この記事では,
- 余因子と余因子展開
- 行列式による正則条件と逆行列
を順に説明します.
なお,この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが,複素行列など一般の体を成分とする行列・ベクトルに対しても同様です.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
余因子と余因子展開
結論から言えば,正方行列$A$に対して$A$が正則行列であるための必要十分条件は$|A|\neq0$ですが,このことを証明するには余因子を説明する必要があります.
余因子
$n$次正方行列$A$に対して,$A$の第$i$行と第$j$列を取り除いてできる${n-1}$次行列の行列式を$(i,j)$小行列式(minor determinant)といい,$(i,j)$小行列式に$(-1)^{i+j}$をかけたものを$(i,j)$余因子(cofactor)という.
この記事では,行列$A=(a_{ij})$の$(i,j)$余因子を$a_{ij}^{*}$と表します.
例えば,$A=\bmat{1&2&3\\4&5&6\\7&8&9}$に対して
\begin{align*}&a_{12}^{*}=(-1)^{1+2}\vmat{4&6\\7&9}=6,
\\&a_{33}^{*}=(-1)^{3+3}\vmat{1&2\\4&5}=-3\end{align*}
ですね.
$n$次正方行列$A$に対して,$A$の$(i,j)$余因子$a_{ij}^{*}$は$A$の第$j$列を$\m{e}_{i}$に置き換えてできる行列の行列式に等しい:
\begin{align*}a_{ij}^{*}=|\m{a}_{1},\dots,\m{a}_{j-1},\m{e}_{i},\m{a}_{j+1},\dots,\m{a}_{n}|\end{align*}
行列$[\m{a}_{1},\dots,\m{a}_{j-1},\m{e}_{i},\m{a}_{j+1},\dots,\m{a}_{n}]$を
\begin{align*}[\m{a}_{1},\dots,\m{a}_{j-1},\m{e}_{i},\m{a}_{j+1},\dots,\m{a}_{n}]=\bmat{A_{1}&\m{0}&A_{2}\\\m{p}&1&\m{q}\\A_{1}&\m{0}&A_{2}}\end{align*}
とおく.
$\sigma,\tau\in S_{n}$を巡回置換$\sigma:=(1,\dots,j)$, $\tau:=(1,\dots,i)$とすると
\begin{align*}\vmat{A_{1}&\m{0}&A_{2}\\\m{p}&1&\m{q}\\A_{1}&\m{0}&A_{2}}
&=\sgn{\sigma}\vmat{\m{0}&A_{1}&A_{2}\\1&\m{p}&\m{q}\\\m{0}&A_{1}&A_{2}}
=\sgn{\sigma}\sgn{\tau}\vmat{1&\m{p}&\m{q}\\\m{0}&A_{1}&A_{2}\\\m{0}&A_{1}&A_{2}}
\\&=(-1)^{i+j-2}\vmat{A_{1}&A_{2}\\A_{1}&A_{2}}=(-1)^{i+j}\vmat{A_{1}&A_{2}\\A_{1}&A_{2}}=a_{ij}^{*}\end{align*}
を得る.
余因子展開
次の命題は余因子展開(cofactor expansion)とよばれ,理論上非常に有用です.
[余因子展開]$n$次正方行列$A=(a_{ij})$の行列式は,任意の$j=1,2,\dots,n$に対して,以下が成り立つ.
\begin{align*}|A|=\sum_{i=1}^{n}a_{ij}a_{ij}^{*}\bra{=a_{1j}a_{1j}^{*}+\dots+a_{nj}a_{nj}^{*}}\end{align*}
$A=[\m{a}_{1},\dots,\m{a}_{n}]$とすると,行列式の線形性と補題より
\begin{align*}|A|&=\abs{\m{a}_{1},\dots,\m{a}_{j-1},\sum_{i=1}^{n}a_{ij}\m{e}_{i},\m{a}_{j+1},\dots,\m{a}_{n}}
\\&=\sum_{i=1}^{n}a_{ij}\abs{\m{a}_{1},\dots,\m{a}_{j-1},\m{e}_{i},\m{a}_{j+1},\dots,\m{a}_{n}}
\\&=\sum_{i=1}^{n}a_{ij}a_{ij}^{*}\end{align*}
を得る.
例えば,$A=(a_{ij})=\bmat{1&2&3\\4&5&6\\7&8&9}$に対して
\begin{align*}|A|&=a_{11}a_{11}^{*}+a_{21}a_{21}^{*}+a_{31}a_{31}^{*}
\\&=1\cdot(-1)^{1+1}\vmat{5&6\\8&9}+4\cdot(-1)^{2+1}\vmat{2&3\\8&9}+7\cdot(-1)^{3+1}\vmat{2&3\\5&6}
\\&=1\cdot(-1)^{2}\cdot(-3)+4\cdot(-1)^{3}\cdot(-6)+7\cdot(-1)^{4}\cdot(-3)
\\&=-3+24-21=0\end{align*}
と余因子展開から行列式$|A|$が計算できるわけですね.
余因子展開は理論上では非常に重要ですが,実際に行列式を計算する際には前回の記事で説明した基本変形による方法が便利でしょう.
行列式による正則条件と逆行列
余因子を用いることで,次のように正則行列の逆行列を求めることができます.
$n$次正方行列$A$に対して,次は同値である.
- $A$は正則である.
- $|A|\neq0$が成り立つ.
さらに,これらの少なくとも一方,すなわち両方をみたすとき,以下が成り立つ.
\begin{align*}A^{-1}=\frac{1}{|A|}\bmat{a_{11}^{*}&\dots&a_{n1}^{*}\\\vdots&\ddots&\vdots\\a_{1n}^{*}&\dots&a_{nn}^{*}}\end{align*}
$A$が正則であることと$\rank{A}=n$は同値で,これは$A$の簡約化が$n$次単位行列$I_n$であることと同値である.
行列式が0なら行基本変形を施しても行列式は0であるし,行列式が0でないなら行基本変形を施しても行列式は0でないから$(1)\iff(2)$が成り立つ.
また,$A=(a_{ij})=[\m{a}_{1},\dots,\m{a}_{n}]$, $B:=\bmat{a_{11}^{*}&\dots&a_{n1}^{*}\\\vdots&\ddots&\vdots\\a_{1n}^{*}&\dots&a_{nn}^{*}}$とすると,積$BA$の第$(i,j)$成分は
\begin{align*}\sum_{k=1}^{n}a_{kj}a_{ki}^{*}
&=\sum_{k=1}^{n}a_{kj}|\m{a}_{1},\dots,\m{a}_{i-1},\m{e}_{k},\m{a}_{i-1},\m{a}_{n}|
\\&=\abs{\m{a}_{1},\dots,\m{a}_{i-1},\sum_{k=1}^{n}a_{kj}\m{e}_{k},\m{a}_{i-1},\m{a}_{n}}
\\&=\abs{\m{a}_{1},\dots,\m{a}_{i-1},\m{a}_{j},\m{a}_{i-1},\m{a}_{n}}\end{align*}
である.これは
- $i\neq j$のときは,第$i$列と第$j$列が等しいから交代性の系より0に等しく,
- $i=j$のときは,$|A|$に等しい.
よって,$AB=|A|I$となるから,$|A|\neq0$なら$\frac{1}{|A|}B$はAの逆行列となり,$A$は正則である.
例えば,2次行列$A=(a_{ij})=\bmat{a&b\\c&d}$について
\begin{align*}&a_{11}^{*}=(-1)^{1+1}d=d,\quad
a_{12}^{*}=(-1)^{1+2}c=-c,
\\&a_{21}^{*}=(-1)^{2+1}b=-b,\quad
a_{22}^{*}=(-1)^{2+2}a=a\end{align*}
なので,いまの逆行列の定理から$|A|=ad-bc\neq0$なら$A$は正則で
\begin{align*}A^{-1}&=\frac{1}{|A|}\bmat{a_{11}^{*}&a_{21}^{*}\\a_{12}^{*}&a_{22}^{*}}
\\&=\frac{1}{ad-bc}\bmat{d&-b\\-c&a}\end{align*}
となりますね.これは以前の記事から考えていたものと一致していますね.

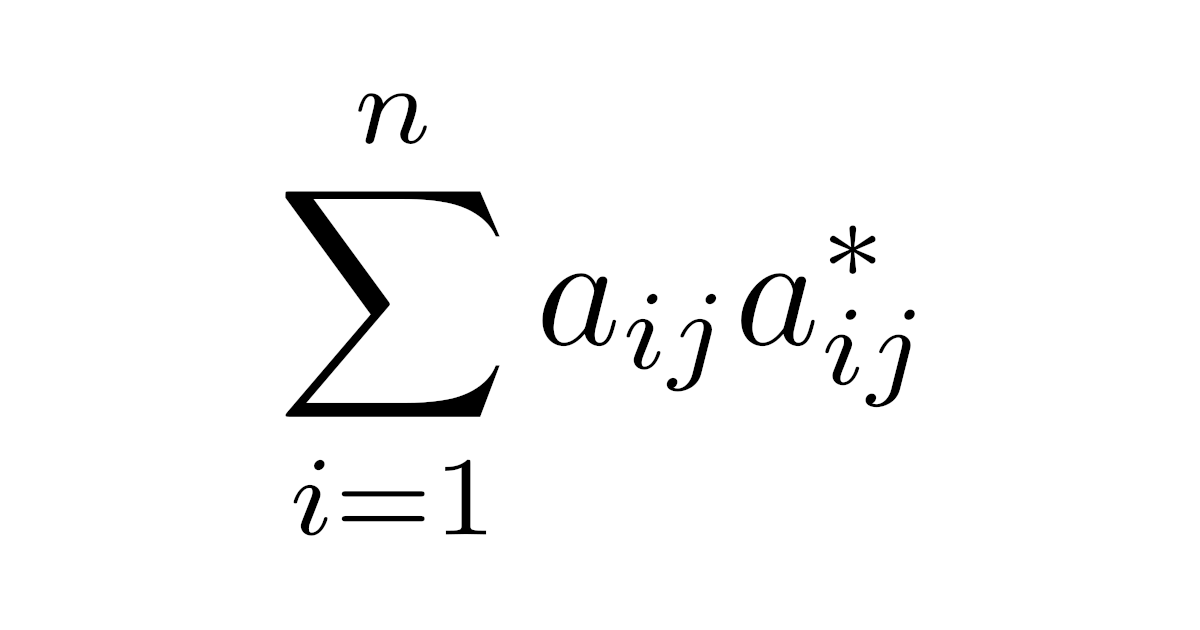


コメント