正方行列の対角化はできればとても便利ですが,残念ながらどんな正方行列でも対角化できるわけではありません.
そのため,正方行列が対角化可能であるかが判定できる方法があると嬉しいですね.
実は$n$次正方行列が異なる$n$個の固有値を持てば,その時点で対角化可能であることが従います.また,どのように対角化されるかが計算しなくても分かります.
この記事では
- 対角化可能性の基本定理と具体例
- 対角化可能性の基本定理の証明
を順に説明します.
なお,この記事では特に断らない限り複素行列・複素ベクトルを扱います.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
対角化可能性の基本定理
最初に冒頭で紹介した正方行列が対角化可能であることが簡単に分かる場合の定理を紹介し,具体例を考えましょう.
定理
次の定理がこの記事の主定理です.
$n$次正方行列$A$が異なる$n$個の固有値$\lambda_1,\lambda_2,\dots,\lambda_n$をもつなら,$A$は対角化可能である.
また,$A$の固有値$\lambda_1,\lambda_2,\dots,\lambda_n$それぞれに属する固有ベクトルを1つずつ取り$\m{p}_1,\dots,\m{p}_n$とすると,
\begin{align*}P=[\m{p}_1,\m{p}_2,\dots,\m{p}_n]\end{align*}
は正則行列となり,この$P$により$A$が対角化できる:
\begin{align*}P^{-1}AP=\bmat{\lambda_1&0&\dots&0\\0&\lambda_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\lambda_n}\end{align*}
つまり,$n$次正方行列$A$が異なる固有値を$n$個もてば,その時点で$A$は対角化可能であること分かるわけですね.
さらに,それぞれの固有値に属する固有ベクトルを並べてできる正方行列$P$により$A$は対角化でき,$P^{-1}AP$の対角行列の成分は全て固有値になるということも併せて理解しておきましょう.
$n$次正方行列が異なる固有値を$n$個もたなくても対角化可能であることもありますが,そのような場合については次の記事で解説しています.
具体例1(2次正方行列)
正方行列$A=\bmat{1&2\\2&1}$を対角化せよ.また,$A$を対角化する正則行列$P$を1つ求めよ.
この正方行列$A$の固有値は$-1,3$で
- 固有値$-1$に属する固有ベクトルは$c\bmat{1\\-1}$($c\neq0$)
- 固有値3に属する固有ベクトルは$d\bmat{1\\1}$($d\neq0$)
であることは前回の記事で示した.
よって,正方行列$A$は異なる固有値を2個もつ2次正方行列だから,上で示した対角化可能性の基本定理より対角化可能である.
さらに,例えば$c=d=1$とすると
- 固有値$-1$に属する固有ベクトル$\bmat{1\\-1}$
- 固有値3に属する固有ベクトル$\bmat{1\\1}$
が得られ,これらの固有ベクトルを並べて$P=\bmat{1&1\\-1&1}$とすると,上の定理より
\begin{align*}P^{-1}AP=\bmat{-1&0\\0&3}\end{align*}
と対角化可能である.
わざわざ$P^{-1}AP$を計算しなくても,固有値が対角成分に並ぶことが分かるのは強力ですね.
$P$に並べる列ベクトルは固有ベクトルであればいいので,例えば$P=\bmat{2&3\\-2&3}$や$P=\bmat{-2&-\pi\\2&-\pi}$などとしても
\begin{align*}P^{-1}AP=\bmat{-1&0\\0&3}\end{align*}
と対角化可能されます.
また,$P$に並べる固有ベクトルの順番と$P^{-1}AP$の対角成分の順番は対応するので,例えば$P=\bmat{-1&1\\1&1}$と固有ベクトルを逆に並べた場合は対角化も
\begin{align*}P^{-1}AP=\bmat{3&0\\0&-1}\end{align*}
と対角成分の固有値は逆になります.
具体例2(3次正方行列)
3次正方行列に対して,固有値・固有ベクトルを求めるところから対角化まで通してみましょう.
正方行列$A=\bmat{2&-2&0\\0&-1&0\\3&0&1}$を対角化せよ.また,$A$を対角化する正則行列$P$を1つ求めよ.
正方行列$A$の固有多項式は
\begin{align*}|xI-A|=&\vmat{x-2&2&0\\0&x+1&0\\-3&0&x-1}
\\=&(x-2)(x+1)(x-1)\end{align*}
なので,固有方程式$|xI-A|=0$の解は$2,1,-1$である.
よって,正方行列$A$は異なる固有値を3個もつ3次正方行列だから,上で示した対角化可能性の基本定理より対角化可能である.
さらに,固有値$2,1,-1$それぞれに属する固有ベクトル$\m{p}_1,\m{p}_2,\m{p}_3$を任意にとり,$P=[\m{p}_1,\m{p}_2,\m{p}_3]$とおくと
\begin{align*}P^{-1}AP=\bmat{2&0&0\\0&1&0\\0&0&-1}\quad\dots(*)\end{align*}
と対角化される.よって,あとは$\m{p}_1,\m{p}_2,\m{p}_3$を求めればよい.
[1] 固有値2に属する固有ベクトル$\m{p}_1$は$A\m{p}_1=2\m{p}_1\iff(A-2I)\m{p}_1=\m{0}$を満たし,行基本変形より
\begin{align*}A-2I=\bmat{0&-2&0\\0&-3&0\\3&0&-1}\to\bmat{3&0&-1\\0&1&0\\0&0&0}\end{align*}
となるから,掃き出し法より$\m{p}_1=c_1\bmat{1\\0\\3}$ ($c_1\neq0$)である.
[2] 固有値1に属する固有ベクトル$\m{p}_2$は$A\m{p}_2=1\m{p}_2\iff(A-I)\m{p}_2=\m{0}$を満たし,行基本変形より
\begin{align*}A-I=\bmat{1&-2&0\\0&-2&0\\3&0&0}\to\bmat{1&0&0\\0&1&0\\0&0&0}\end{align*}
となるから,掃き出し法より$\m{p}_2=c_2\bmat{0\\0\\1}$ ($c_2\neq0$)である.
[3] 固有値$-1$に属する固有ベクトル$\m{p}_3$は$A\m{p}_3=(-1)\m{p}_3\iff(A+I)\m{p}_3=\m{0}$を満たし,
\begin{align*}A+I=\bmat{3&-2&0\\0&0&0\\3&0&2}\end{align*}
となるから,$\m{p}_3=c_3\bmat{2\\3\\-3}$ ($c_3\neq0$)である.
以上より,[1]-[3]で例えば$c_1=c_2=c_3=1$として得られる固有ベクトルを並べた$P=\bmat{1&0&2\\0&0&3\\3&1&-3}$によって,$A$は$(*)$と対角化可能である.
対角化可能性の基本定理の証明
まずは定理の証明の鍵となる命題を示し,上の定理を証明しましょう.
異なる固有値に属する固有ベクトル
正方行列$A$の異なる固有値$\lambda_1,\dots,\lambda_r$に対して,それぞれの固有値に属する固有ベクトルを$\m{a}_1,\dots,\m{a}_r$とすると,$\m{a}_1,\dots,\m{a}_r$は線形独立である.
数学的帰納法により示す.一般にただひとつのベクトルは線形独立なので$\m{a}_1$は線形独立である.
$\m{a}_1,\dots,\m{a}_m$($m<r$)は線形独立であると仮定する.線形関係
\begin{align*}c_1\m{a}_1+\dots+c_{m+1}\m{a}_{m+1}=\m{0}\quad\dots(*)\end{align*}
を考える.線形関係$(*)$の両辺に左から$T$を施して
\begin{align*}& \lambda_{1}c_1\m{a}_1+\dots+\lambda_{m+1}c_{m+1}\m{a}_{m+1}=\m{0}\end{align*}
であり,線形関係$(*)$の両辺に$\lambda_{m+1}$をかけて
\begin{align*}\lambda_{m+1}c_1\m{a}_1+\dots+\lambda_{m+1}c_{m+1}\m{a}_{m+1}=\m{0}\end{align*}
である.これら2式の辺々引いて
\begin{align*}(\lambda_{m+1}-\lambda_{1})c_1\m{a}_1+\dots+(\lambda_{m+1}-\lambda_{m})c_{m}\m{a}_{m}=\m{0}\end{align*}
となる.帰納法の仮定より$\m{a}_1,\dots,\m{a}_{m}$は線形独立なので$(\lambda_{m+1}-\lambda_k)c_k=0$($k=1,\dots,m$)が成り立つ.
固有値$\lambda_1,\dots,\lambda_{m+1}$は異なると仮定していたから,$\lambda_{r+1}-\lambda_k\neq0$なので$c_k=0$を得る.
これをもとの線形関係$(*)$に代入すると$c_{m+1}\m{a}_{m+1}=0$となるから,$\m{a}_{m+1}\neq\m{0}$より$c_{m+1}=0$を得る.
よって,$\m{a}_1,\dots,\m{a}_r,\m{a}_{m+1}$も線形独立である.
この命題から次が成り立ちますね.
$n$次正方行列$A$が異なる$n$個の固有値をもつとき,それぞれの固有値に属する固有ベクトルを1つずつ取り$\m{p}_1,\dots,\m{p}_n$とすると,正方行列$[\m{p}_1,\dots,\m{p}_n]$は正則行列である.
一般に$\m{a}_1,\dots,\m{a}_n\in\C^n$が線形独立なら正方行列$[\m{a}_1,\dots,\m{a}_n]$は正則である.
また,上で示した命題から$\m{p}_1,\dots,\m{p}_n$は線形独立だから,$n$次正方行列$P=[\m{p}_1,\dots,\m{p}_n]$は正則行列である.
定理の証明
それでは本題の定理を証明しましょう.
$n$次正方行列$A$が異なる$n$個の固有値$\lambda_1,\lambda_2,\dots,\lambda_n$をもつとする.
このとき,$A$の固有値$\lambda_1,\lambda_2,\dots,\lambda_n$それぞれに属する固有ベクトルを1つずつ取り$\m{p}_1,\dots,\m{p}_n$とすると,
\begin{align*}P=[\m{p}_1,\m{p}_2,\dots,\m{p}_n]\end{align*}
は正則行列となり,この$P$によって$A$は
\begin{align*}P^{-1}AP=\bmat{\lambda_1&0&\dots&0\\0&\lambda_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\lambda_n}\end{align*}
と対角化可能である.
対角行列$B$を
\begin{align*}B=\bmat{\lambda_1&0&\dots&0\\0&\lambda_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\lambda_n}\end{align*}
で定める.固有値・固有ベクトルの定義より$\lambda_k\m{p}_k=A\m{p}_k$ ($k=1,2,\dots,n$)が成り立つから,
\begin{align*}PB=&[\m{p}_1,\m{p}_2,\dots,\m{p}_n]\bmat{\lambda_1&0&\dots&0\\0&\lambda_2&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&\lambda_n}
\\=&[\lambda_1\m{p}_1,\lambda_2\m{p}_2,\dots,\lambda_n\m{p}_n]
=[A\m{p}_1,A\m{p}_2,\dots,A\m{p}_n]
\\=&A[\m{p}_1,\m{p}_2,\dots,\m{p}_n]
=AP\end{align*}
となる.いま$\lambda_1,\dots,\lambda_n$は全て異なるから,上で示した系より$P=[\m{p}_1,\dots,\m{p}_n]$は正則行列である.
よって,$PB=AP$の両辺に左から$P^{-1}$をかけて$B=P^{-1}AP$と対角化可能である.
証明を読んでみると$\m{p}_1,\m{p}_2,\dots,\m{p}_n$が線形独立でない場合でも$PB=AP$までは成り立ちますね.
そこから$B=P^{-1}AP$の形に変形するには$P$が正則行列でなければならず,それは$A$が異なる固有値を$n$個もつことから従うわけですね.

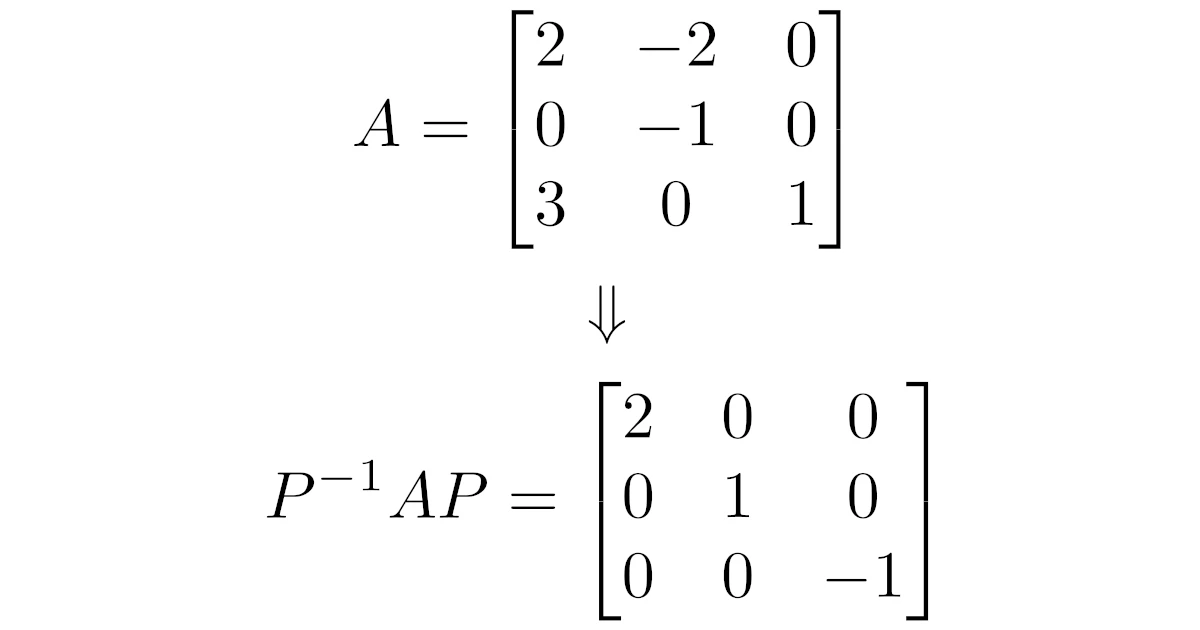


コメント