2次正方行列$A=\bmat{a&b\\c&d}$の行列式$\det{A}$は$\det{A}=ad-bc$と定義され,$\det{A}$が0であるか否かで行列$A$が正則行列であるかどうかを判定できるのでした.
さて,3次以上でも0であるか否かで正則性が判定できる行列式を定義できますが,その定義のためには置換を用いるのが一般的です.
この記事では
- 置換の符号(偶置換・奇置換)
- 行列式の定義と具体例
- 互換の個数の偶奇が一定であることの証明
を順に解説します.
なお,この記事では特に断らない限り実行列・実ベクトルを扱うことにしますが,複素行列など一般の体を成分とする行列・ベクトルに対しても同様です.
また,この記事では$n$を2以上の整数とし,$\{1,\dots,n\}$の置換全部の集合を$S_n$とします.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
置換の符号(偶置換・奇置換)
正方行列の行列式を定義するために置換の符号が必要なので定義しておきましょう.
互換の積としての置換
置換に関して次の定理が成り立つのでした.
例えば,$\{1,2,3,4\}$の置換$\sigma=\pmat{1&2&3&4\\2&3&4&1}$は
\begin{align*}\sigma=(1,4)(1,3)(1,2)\end{align*}
などと表すことができますね.ただし,$(i,j)$で$i$と$j$の互換を表します.他にも
\begin{align*}\sigma=(3,4)(3,4)(1,4)(1,3)(1,2)\end{align*}
と表すこともできますね.
置換の符号の定義
いまの例から分かるように,置換を互換の積で表すときの互換の個数は一定ではありません.しかし,置換を互換の積でどのように表しても互換の個数の偶奇が一定であることは証明することができます.
置換を互換の積で表すとき,かけ合わされている互換の個数の偶奇は各置換に固有である.
証明は少々テクニカルなのでこの記事の最後に残すことにし,ここで置換の符号を定義しましょう.
置換$\sigma$が偶数個の互換の積で表されるとき$\sigma$を偶置換(even permutation)といい,奇数個の互換の積で表されるとき$\sigma$を奇置換(odd permutation)という.
$\sigma$が偶置換のとき$\sgn(\sigma)=1$と表し,$\sigma$が奇置換のとき$\sgn(\sigma)=-1$と表す.$\sgn(\sigma)$を$\sigma$の符号(signature)という.
ひとつの置換を互換の積で表す方法は複数あり得ますが,上の定理よりそのときの互換の個数の偶奇はどの表し方でも変わらないので,このように定義できるわけですね.このように複数の表し方がある場合,どの表し方でも同じ定義になることをwell-definedと言います.
置換の符号の具体例
$\{1,2,3\}$の置換を全て挙げ,各置換の符号を答えよ.
$\{1,2,3\}$の置換を全て挙げると
\begin{align*}&\sigma_1:=\pmat{1&2&3\\1&2&3},\sigma_2:=\pmat{1&2&3\\1&3&2},\sigma_3:=\pmat{1&2&3\\2&1&3},
\\&\sigma_4:=\pmat{1&2&3\\3&1&2},\sigma_5:=\pmat{1&2&3\\2&3&1},\sigma_6:=\pmat{1&2&3\\3&2&1}\end{align*}
で,これらは
\begin{align*}&\sigma_1=(1,2)(1,2),\quad\sigma_2=(2,3),\quad\sigma_3=(1,2),
\\&\sigma_4=(2,3)(1,2),\quad\sigma_5=(1,3)(1,2),\quad\sigma_6=(1,3)\end{align*}
と互換の積で表せるので
\begin{align*}&\sgn(\sigma_1)=\sgn(\sigma_4)=\sgn(\sigma_5)=1,
\\&\sgn(\sigma_2)=\sgn(\sigma_3)=\sgn(\sigma_6)=-1\end{align*}
である.
行列式の定義と具体例
それでは本題の行列式を定義しましょう.
$n$次正方行列$A$に対して
\begin{align*}\sum_{\sigma\in S_n}\sgn(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}\end{align*}
を$A$の行列式(determinant)といい,$|A|$や$\det{A}$と表す.
$\{1,2,\dots,n\}$の置換は全部で$n!$個あるので,この和は$n!$個の項の和となっています.すぐには捉えづらいと思うので,具体的に$n=2,3$の場合を考えてみましょう.
具体例1(2次正方行列の行列式)
2次正方行列$A=\bmat{a_{11}&a_{12}\\a_{21}&a_{22}}$の行列式$|A|$を考えます.
$S_2$は$\{1,2\}$の置換全体の集合だから
\begin{align*}S_2=\brb{\sigma_{1}:=\pmat{1&2\\1&2},\sigma_{2}:=\pmat{1&2\\2&1}}\end{align*}
です.$\sgn(\sigma_{1})=1$, $\sgn(\sigma_{2})=-1$より
\begin{align*}|A|=&\sgn(\sigma_{1})a_{1\sigma_{1}(1)}a_{2\sigma_{1}(2)}+\sgn(\sigma_{2})a_{1\sigma_{2}(1)}a_{2\sigma_{2}(2)}
\\=&a_{11}a_{22}-a_{12}a_{21}\end{align*}
となります.これは以前の記事で説明した2次正方行列の行列式に一致しますね.
たとえば具体的に$A=\bmat{1&2\\3&4}$とすると,
\begin{align*}|A|=1\cdot4-2\cdot3=-2\end{align*}
となりますね.
具体例2(3次正方行列の行列式)
3次正方行列$A=\bmat{a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}}$の行列式$|A|$を考えます.
3次の置換の集合$S_3$は
\begin{align*}S_3=\left\{\sigma_{1}:=\pmat{1&2&3\\1&2&3},\sigma_{2}:=\pmat{1&2&3\\1&3&2},\sigma_{3}:=\pmat{1&2&3\\2&1&3},\right.&
\\\left.\sigma_{4}:=\pmat{1&2&3\\2&3&1},\sigma_{5}:=\pmat{1&2&3\\3&1&2},\sigma_{6}:=\pmat{1&2&3\\3&2&1}\right\}&\end{align*}
で,$\sgn(\sigma_{1})=1$, $\sgn(\sigma_{2})=-1$, $\sgn(\sigma_{3})=-1$, $\sgn(\sigma_{4})=1$, $\sgn(\sigma_{5})=1$, $\sgn(\sigma_{6})=-1$より
\begin{align*}|A|=&\sgn{(\sigma_{1})}a_{1\sigma_{1}(1)}a_{2\sigma_{1}(2)}a_{3\sigma_{1}(3)}+\sgn{(\sigma_{2})}a_{1\sigma_{2}(1)}a_{2\sigma_{2}(2)}a_{3\sigma_{2}(3)}
\\&+\sgn{(\sigma_{3})}a_{1\sigma_{3}(1)}a_{2\sigma_{3}(2)}a_{3\sigma_{3}(3)}+\sgn{(\sigma_{4})}a_{1\sigma_{4}(1)}a_{2\sigma_{4}(2)}a_{3\sigma_{4}(3)}
\\&+\sgn{(\sigma_{5})}a_{1\sigma_{5}(1)}a_{2\sigma_{5}(2)}a_{3\sigma_{5}(3)}+\sgn{(\sigma_{6})}a_{1\sigma_{6}(1)}a_{2\sigma_{6}(2)}a_{3\sigma_{6}(3)}
\\=&a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}
\\&-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}\end{align*}
となります.
たとえば具体的に$A=\bmat{1&2&3\\4&5&6\\7&8&9}$とすると,
\begin{align*}|A|&=1\cdot5\cdot9+2\cdot6\cdot7+3\cdot4\cdot8
\\&\quad-3\cdot5\cdot7-2\cdot4\cdot9-1\cdot6\cdot8
\\&=45+84+96-48-105-72=0\end{align*}
となりますね.
互換の個数の偶奇が一定であることの証明
それでは最後に置換の符号の定義のベースとなった次の定理を証明しましょう.
(再掲)置換を互換の積で表すとき,かけ合わされている互換の個数の偶奇は各置換に固有である.
異なる$x_{1},\dots,x_{n}\in\R$に対して,写像$f:S_{n}\to\R$を$f(\sigma):=\prod_{i<j}(x_{\sigma(i)}-x_{\sigma(j)})$で定める.すなわち,
\begin{align*}f(\sigma)
=(x_{\sigma(1)}-x_{\sigma(2)})(x_{\sigma(1)}-x_{\sigma(3)})
\times\dots\times(x_{\sigma(1)}-x_{\sigma(n)})&
\\\times(x_{\sigma(2)}-x_{\sigma(3)})\times\dots\times(x_{\sigma(2)}-x_{\sigma(n)})&
\\\vdots\qquad&
\\\times(x_{\sigma(n-1)}-x_{\sigma(n)})&\end{align*}
である.ここで,偶数$k$個の互換の積と奇数$\ell$個の互換の積で表せる置換$\sigma$が存在すれば,
\begin{align*}\sigma=\tau_{1}\dots\tau_{k}=\iota_{1}\dots\iota_{\ell}\end{align*}
と表せる.ただし,$\tau_{i},\iota_{j}\in S_{n}$ ($i=1,\dots,k$, $j=1,\dots,\ell$)は互換である.
任意の互換$\eta:=(i,j)\in S_{n}$と置換$\kappa\in S_{n}$に対して,$f(\kappa\eta)$は$f(\kappa)$の因数のうち奇数個の符号が逆になったものなので$f(\kappa\eta)=-f(\kappa)$である.
$k+\ell$が奇数であることに注意すると,
\begin{align*}f(\epsilon)=&-f(\tau_{1})=(-1)^{2}f(\tau_{1}\tau_{2})
\\=&\dots=(-1)^{k}f(\tau_{1}\dots\tau_{k})=(-1)^{k}f(\iota_{1}\dots\iota_{\ell})
\\=&(-1)^{k+1}f(\iota_{2}\dots\iota_{\ell})=\dots=(-1)^{k+\ell-1}f(\iota_{\ell})
\\=&(-1)^{k+\ell}f(\epsilon)=-f(\epsilon)\end{align*}
となって,$f(\epsilon)=0$を得る.しかし,$x_{1},\dots,x_{n}$は全て異なるとしたから,$f(\epsilon)\neq0$なのでこれは矛盾である.
よって,$\sigma$を互換の積で表すとき,互換の個数の偶奇は固有である.
この証明の写像$f$は差積(difference product)やヴァンデルモンド多項式(Vandermonde polynomial)などと呼ばれます.

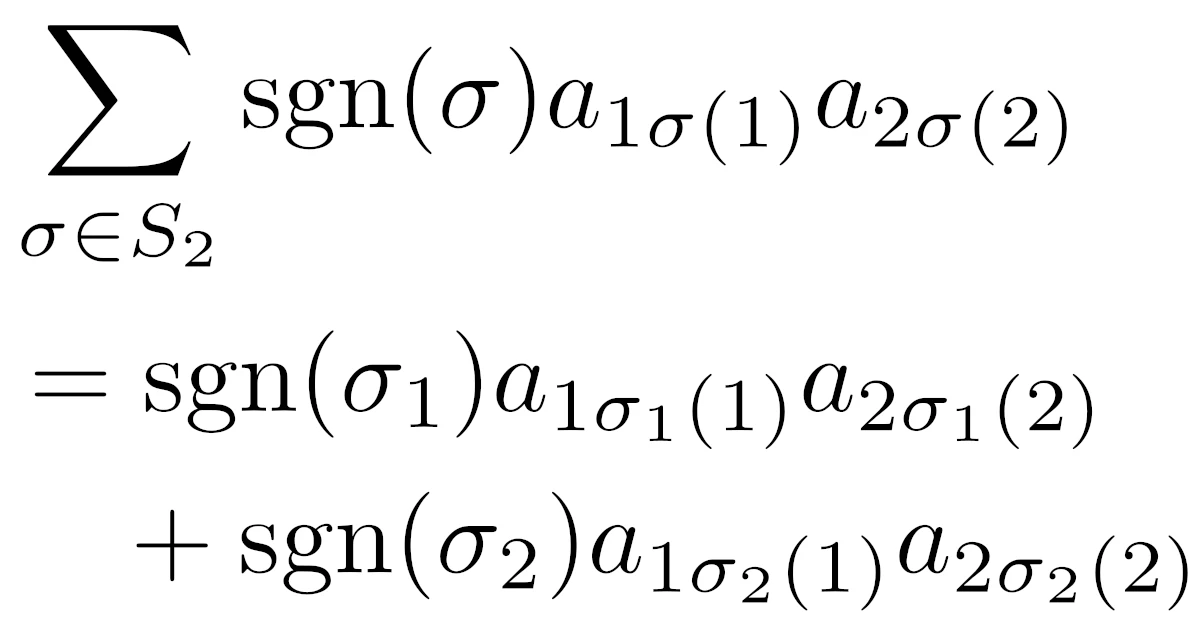


コメント