$n$次列ベクトル全部の空間$\R^n$の2つの部分空間$U$, $V$の共通部分$U\cap V$は$\R^n$の部分空間となります.共通部分は2つの集合の重なっている部分なので,共通部分$U\cap V$はもとの$U$, $V$に含まれる部分空間となっています.
一方,2つの部分空間$U$, $V$を併せた部分空間として和空間というものが定義され,和空間$U+V$はもとの$U$, $V$を含む部分空間となっています.
この記事では
- $\R^n$の部分空間の和空間
- 部分空間の和空間の具体例
- 補足(和空間と和集合との違い)
を順に解説します.
なお,特に断らない限り以下では実行列・実ベクトルを扱うことにしますが,複素行列など一般の体を成分とする行列・ベクトルに対しても同様です.
この記事の内容は一般の線形空間でも同様に成り立ちますが,簡単のためここでは$\R^n$の部分空間に限って話を進めます.
「線形代数学の基本」の一連の記事
- 行列と列ベクトル
- 行列式
- $\R^n$の部分空間と基底
$\R^n$の部分空間の和空間
$\R^n$の2つの部分空間$U$, $V$それぞれから列ベクトルを取り出し,足し合わせてできるベクトル全部の集合を$U$, $V$の和空間といいます.
$\R^n$の部分空間の和空間の定義
$\R^n$の部分空間$U$, $V$に対して,集合
\begin{align*}U+V:=\set{\m{u}+\m{v}}{\m{u}\in U,\m{v}\in V}\end{align*}
を$U$, $V$の和空間(sum)という.
この記事では2つの部分空間の和空間のみ扱いますが,3つ以上の部分空間の和空間についても帰納的に和空間が定義されます.
$U,V\subset\R^n$なので$\m{u}\in U$も$\m{v}\in V$も$\R^n$に属しますね.よって,これらの和$\m{u}+\m{v}$も$\R^n$に属しますから,和空間$U+V$は$\R^n$の部分集合ですね.
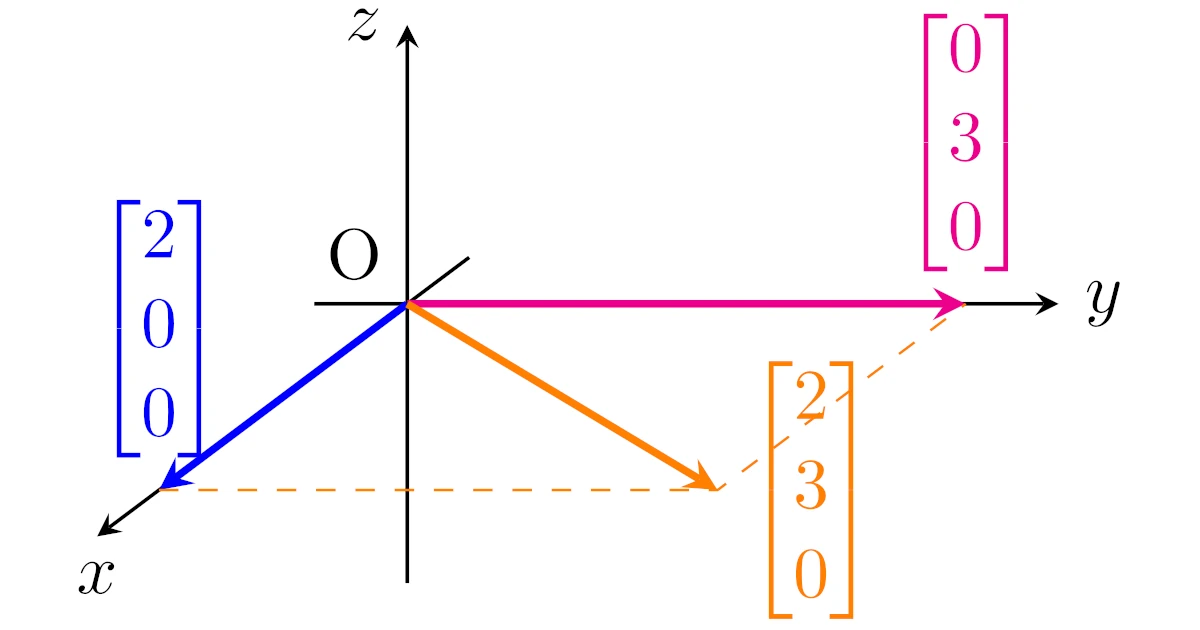
具体例1($\R^3$上の$x$軸と$y$軸の和空間)
$\R^3$の部分空間$U$, $V$を
\begin{align*}U=\set{\bmat{x\\0\\0}}{x\in\R},\quad
V=\set{\bmat{0\\y\\0}}{y\in\R}\end{align*}
とするとき,和空間$U+V$の次元$\dim{(U+V)}$を求めよ.
$U$は$\R^3$の$x$軸,$V$は$\R^3$の$y$軸ですね.$U$の列ベクトルと$V$の列ベクトルを足し合わせてできるベクトルを全て集めてできる集合が$U+V$なので,例えば
\begin{align*}\bmat{2\\0\\0}\in U,\quad\bmat{0\\3\\0}\in V\end{align*}
を足し合わせてできる$\bmat{2\\3\\0}$は和空間$U+V$の元です.
この他にも$U$, $V$の列ベクトルはたくさんあり,それらのありとあらゆる和を全て考えてできる列ベクトル全部の集合というわけですね.このように考えると,和空間$U+V$は$xy$平面(2次元)となりそうなことが見てとれますね.
和空間の定義と$U$, $V$の定め方より
\begin{align*}U+V&=\set{\m{u}+\m{v}}{\m{u}\in U,\m{v}\in V}
\\&=\set{\sbmat{x\\0\\0}+\sbmat{0\\y\\0}}{x\in\R,y\in\R}
\\&=\set{x\sbmat{1\\0\\0}+y\sbmat{0\\1\\0}}{x,y\in\R}
\\&=\spn{\bra{\sbmat{1\\0\\0},\sbmat{0\\1\\0}}}\end{align*}
と和空間$U+V$は$\sbmat{1\\0\\0},\sbmat{0\\1\\0}$により生成される部分空間である.また,一般に零ベクトルでない2つのベクトルは平行でなければ線形独立だから$\sbmat{1\\0\\0},\sbmat{0\\1\\0}$は線形独立である.
よって,$U+V$の基底として$\anb{\sbmat{1\\0\\0},\sbmat{0\\1\\0}}$がとれることが分かった.$U+V$の基底をなすベクトルの個数が2なので
\begin{align*}\dim{(U+V)}=2\end{align*}
である.
$\R^n$の部分空間の和空間は$\R^n$の部分空間
いまの具体例1で見てとれるように,部分空間$U,V\subset\R^n$の和空間$U+V$は$\R^n$の部分空間であることが証明できます.
$\R^n$の部分空間$U$, $V$の和空間$U+V$は$\R^n$の部分空間となる.
$U$, $V$は$\R^n$の部分空間で,$\R^n$の任意の部分空間は零ベクトル$\m{0}_n$を元にもつから,$\m{0}_n\in U$かつ$\m{0}_n\in V$が成り立つ.よって,
\begin{align*}\m{0}_n=\m{0}_n+\m{0}_n\in U+V\end{align*}
だから,$U+V$は空でない.よって,あとは$U+V$が和とスカラー倍について閉じていることを示せばよい.
和について閉じていることの証明
任意に$\m{a},\m{b}\in U+V$をとる.このとき,$U+V$の定義より
\begin{align*}\m{a}=\m{u}_1+\m{v}_1,\quad
\m{b}=\m{u}_2+\m{v}_2\end{align*}
なる$\m{u}_1,\m{u}_2\in U$, $\m{v}_1,\m{v}_2\in V$が存在する.よって,
\begin{align*}\m{a}+\m{b}=&(\m{u}_1+\m{v}_1)+(\m{u}_2+\m{v}_2)
\\=&(\m{u}_1+\m{u}_2)+(\m{v}_1+\m{v}_2)\end{align*}
であり,$U$, $V$は$\R^n$の部分空間だから$\m{u}_1+\m{u}_2\in U$, $\m{v}_1+\m{v}_2\in V$なので,$\m{a}+\m{b}\in U+V$が成り立つ.
スカラー倍について閉じていることの証明
任意に$\m{a}\in U+V$, $k\in\R$をとる.このとき,$U+V$の定義より$\m{a}=\m{u}+\m{v}$なる$\m{u}\in U$, $\m{v}\in V$が存在する.よって,
\begin{align*}k\m{a}=k(\m{u}+\m{v})=k\m{u}+k\m{v}\end{align*}
であり,$U$, $V$は$\R^n$の部分空間だから$k\m{u}\in U$, $k\m{v}\in V$なので,$k\m{a}\in U+V$が成り立つ.
生成される部分空間の和空間
とくに,部分空間$U,V\subset\R^n$がどのようなベクトルから生成されるかが分かっていれば,和空間$U+V$は簡単に求められます.
$\m{a}_1,\dots,\m{a}_r,\m{b}_1,\dots,\m{b}_s\in\R^n$とする.$\R^n$の部分空間$U$, $V$を
\begin{align*}U&=\spn{(\m{a}_1,\dots,\m{a}_r)},
\\V&=\spn{(\m{b}_1,\dots,\m{b}_s)}\end{align*}
と定める.このとき,和空間$U+V$は
\begin{align*}U+V=\spn{(\m{a}_1,\dots,\m{a}_r,\m{b}_1,\dots,\m{b}_s)}\end{align*}
となる.
部分空間$U$, $V$を生成するベクトルたちを併せて生成される空間が,和空間$U+V$になるというわけですね.
生成される部分空間の定義より
- $U$上のベクトルは$c_1\m{a}_1+\dots+c_r\m{a}_r$($c_1,\dots,c_r\in\R$)
- $V$上のベクトルは$d_1\m{b}_1+\dots+d_s\m{b}_s$($d_1,\dots,d_s\in\R$)
と表すことができるから,和空間$U+V$は
\begin{align*}U+V&=\set{\begin{aligned}&(c_1\m{a}_1+\dots+c_r\m{a}_r)\\&\quad+(d_1\m{b}_1+\dots+d_s\m{b}_s)\end{aligned}}{\begin{aligned}&c_1,\dots,c_r,\\&\quad d_1,\dots,d_s\in\R\end{aligned}}
\\&=\spn{(\m{a}_1,\dots,\m{a}_r,\m{b}_1,\dots,\m{b}_s)}\end{align*}
となる.
部分空間の和空間の具体例
それではいくつか具体例を考えましょう.
具体例2($\R^3$上の直線と直線の和空間)
$\R^3$の部分空間$U$, $V$を
\begin{align*}U=\set{\bmat{t\\t\\0}}{t\in\R},\quad
V=\set{\bmat{0\\y\\0}}{y\in\R}\end{align*}
とするとき,和空間$U+V$の次元$\dim{(U+V)}$を求めよ.
$V$は具体例1と同じく$\R^3$の$y$軸ですが,$U$は第1成分と第2成分が等しく第3成分が0の列ベクトル全部の集合ですね.たとえば,
\begin{align*}\bmat{2\\3\\0}=\bmat{2\\2\\0}+\bmat{0\\1\\0},\quad
\bmat{3\\-4\\0}=\bmat{3\\3\\0}+\bmat{0\\-7\\0}\end{align*}
のように$xy$平面上の列ベクトルは全て$U$の列ベクトルと$V$の列ベクトルの線形結合で表せそうですから,具体例1と同様に和空間$U+V$は$xy$平面(2次元)となりそうですね.
$U$, $V$はそれぞれ
\begin{align*}U=\spn{\bra{\sbmat{1\\1\\0}}},\quad
V=\spn{\bra{\sbmat{0\\1\\0}}}\end{align*}
と表せるから,和空間は$U+V=\spn{\bra{\sbmat{1\\1\\0},\sbmat{0\\1\\0}}}$となる.また,一般に2つのベクトルが平行でなければ線形独立なので$\sbmat{1\\1\\0},\sbmat{0\\1\\0}$は線形独立である.
よって,$\anb{\sbmat{1\\1\\0},\sbmat{0\\1\\0}}$は和空間$U+V$の基底であり,$\dim{(U+V)}=2$である.
具体例3($\R^3$上の平面と直線の和空間)
$\R^3$の部分空間$U$, $V$を
\begin{align*}U=&\set{\bmat{x\\y\\z}\in\R^3}{x+2y-z=0},
\\V=&\set{\bmat{x\\y\\z}\in\R^3}{\begin{aligned}&x+y+z=0,\\&x-y=0\end{aligned}}\end{align*}
とするとき,和空間$U+V$の次元$\dim{(U+V)}$を求めよ.
直線$V$が平面$U$にブスッと突き刺さっているので,$U$, $V$の列ベクトルを足し合わせると$\R^3$上のどんなベクトルも表すことができそうですね.つまり,和空間$U+V$は$\R^3$全体となりそうです.
部分空間$U$は生成される部分空間として
\begin{align*}U=&\set{\sbmat{x\\y\\z}\in\R^3}{x+2y-z=0}=\set{\sbmat{x\\y\\x+2y}}{x,y\in\R}
\\=&\set{x\sbmat{1\\0\\1}+y\sbmat{0\\1\\2}}{x,y\in\R}=\spn{\bra{\sbmat{1\\0\\1},\sbmat{0\\1\\2}}}\end{align*}
と表せる.同様に,部分空間$V$も生成される部分空間として
\begin{align*}V=&\set{\sbmat{x\\y\\z}\in\R^3}{\begin{aligned}&x+y+z=0,\\&x-y=0\end{aligned}}=\set{\sbmat{x\\x\\-2x}}{x\in\R}
\\=&\set{x\sbmat{1\\1\\-2}}{x\in\R}=\spn{\bra{\sbmat{1\\1\\-2}}}\end{align*}
と表せる.よって,和空間は$U+V=\spn{\bra{\sbmat{1\\0\\1},\sbmat{0\\1\\2},\sbmat{1\\1\\-2}}}$となる.これらの列ベクトルを並べてできる行列を行基本変形すると
\begin{align*}\bmat{1&0&1\\0&1&1\\1&2&-2}\to\bmat{1&0&1\\0&1&1\\0&2&-3}\to\bmat{1&0&0\\0&1&0\\0&0&1}\end{align*}
と簡約化できるので,行列$\sbmat{1&0&1\\0&1&1\\1&2&-2}$のランクは3だから$\sbmat{1\\0\\1},\sbmat{0\\1\\2},\sbmat{1\\1\\-2}$は線形独立である.
よって,$\anb{\sbmat{1\\0\\1},\sbmat{0\\1\\2},\sbmat{1\\1\\-2}}$は和空間$U+V$の基底であり,$\dim{(U+V)}=3$である.
具体例4($\R^4$上の平面と平面の和空間)
具体例1から具体例3までは$\dim{(U+V)}=\dim{U}+\dim{V}$となっていましたが,これはいつでも成り立つわけではありません.
$\R^4$の部分空間$U$, $V$を
\begin{align*}U=&\spn{\bra{\bmat{-1\\1\\1\\0},\bmat{5\\-2\\0\\1}}},\quad
V=\spn{\bra{\bmat{2\\1\\0\\1},\bmat{-6\\0\\3\\-2}}}\end{align*}
とするとき,和空間$U+V$の次元$\dim{(U+V)}$を求めよ.
$\R^4$が4次元なので図に描くのは難しいですが,$U$, $V$はともに生成される部分空間として表されているので,いままでの具体例と同様に求めることができますね.
和空間$U+V$は$U+V=\spn{\bra{\sbmat{-1\\1\\1\\0},\sbmat{5\\-2\\0\\1},\sbmat{2\\1\\0\\1},\sbmat{-6\\0\\3\\-2}}}$であり,これらの列ベクトルを並べてできる行列を行基本変形すると
\begin{align*}&\bmat{-1&5&2&-6\\1&-2&1&0\\1&0&0&3\\0&1&1&-2}\to\bmat{1&0&0&3\\0&5&2&-3\\0&-2&1&-3\\0&1&1&-2}
\\\to&\bmat{1&0&0&3\\0&1&1&-2\\0&0&-3&7\\0&0&3&-7}\to\bmat{1&0&0&3\\0&1&1&-2\\0&0&-3&7\\0&0&0&0}\end{align*}
となる.行基本変形で列ベクトルの線形関係は不変だから$\sbmat{-1\\1\\1\\0},\sbmat{5\\-2\\0\\1},\sbmat{2\\1\\0\\1}$は線形独立で,残る$\sbmat{-6\\0\\3\\-2}$はこれらの線形結合で表せる.
よって,$\anb{\sbmat{-1\\1\\1\\0},\sbmat{5\\-2\\0\\1},\sbmat{2\\1\\0\\1}}$は和空間$U+V$の基底であり,$\dim{(U+V)}=3$である.
補足(和空間と和集合との違い)
先ほども少し触れましたが,和集合
\begin{align*}U\cup V=\set{\m{x}\in\R^n}{\m{x}\in U\ \text{または}\ \m{x}\in V}\end{align*}
と和空間$U+V$は異なります.
和集合はただ単に集合を併せてできる集合なので,上の例の$\R^3$上の$x$軸$U$と$y$軸$V$の和集合$U\cup V$は「十字路」のような集合となります.
これは和空間と違って,$\R^3$の部分空間にはなっていませんね.
一般に$\R^n$の部分空間$U$, $V$の和集合$U\cup V$が$\R^n$の部分空間となるための必要十分条件は$U\subset V$または$V\subset U$が成り立つことです.



コメント